น้องๆ หลายคนพอได้ยินคำว่า “Regression Analysis” แล้วใจเริ่มสั่น มือเริ่มเย็นทันทีครับ 😂
บางคนเปิด SPSS มาแล้วกด Analyze แบบขอพรสิ่งศักดิ์สิทธิ์ก่อนทุกครั้ง เพราะกลัวตัวเลขแดง กลัว Sig. ไม่ผ่าน กลัวอาจารย์ถามแล้วตอบไม่ได้ครับ

แต่พี่อยากบอกว่า จริงๆ แล้ว Regression Analysis ไม่ได้น่ากลัวขนาดนั้นครับ ถ้าเราเข้าใจ “บทบาท” ของมันอย่างถูกต้อง มันจะกลายเป็นอาวุธลับที่ช่วยให้งานวิจัยของเรา “ดูมีน้ำหนัก” และ “น่าเชื่อถือ” ขึ้นแบบก้าวกระโดดเลยครับ

บทความนี้พี่จะพาน้องๆ มาดูแบบเข้าใจง่ายว่า Regression Analysis มีบทบาทอะไรในงานวิจัย ใช้ทำอะไรได้บ้าง สำคัญแค่ไหน รวมถึงข้อควรระวังที่นักวิจัยมือใหม่ชอบพลาดกันบ่อยครับ

Regression Analysis คืออะไร ทำไมงานวิจัยยุคนี้แทบขาดไม่ได้

Regression Analysis หรือ “การวิเคราะห์ถดถอย” คือเทคนิคทางสถิติที่ใช้ศึกษาความสัมพันธ์ระหว่าง

• ตัวแปรอิสระ (Independent Variable)
• ตัวแปรตาม (Dependent Variable)

พูดง่ายๆ คือ มันช่วยตอบคำถามว่า

“ปัจจัยอะไร ส่งผลต่อสิ่งที่เราสนใจมากที่สุดครับ”

เช่น

• รายได้ส่งผลต่อการตัดสินใจซื้อไหม
• แรงจูงใจมีผลต่อผลการเรียนหรือเปล่า
• คุณภาพบริการทำให้ลูกค้ากลับมาซื้อซ้ำจริงไหม

Regression Analysis จึงเป็นเหมือน “นักสืบของข้อมูล” ที่ช่วยแกะรอยความสัมพันธ์ต่างๆ ออกมาอย่างเป็นระบบครับ

ทำไม Regression Analysis ถึงสำคัญกับงานวิจัยมาก

หลายคนเข้าใจว่า Regression มีไว้ “คำนวณตัวเลข” อย่างเดียว
แต่จริงๆ แล้วบทบาทของมันลึกกว่านั้นเยอะครับ

เพราะมันช่วยให้นักวิจัยสามารถ

• อธิบายความสัมพันธ์ของตัวแปร
• ทดสอบสมมติฐาน
• ทำนายแนวโน้มในอนาคต
• ควบคุมตัวแปรแทรกซ้อน
• สนับสนุนการตัดสินใจเชิงวิชาการ

พูดง่ายๆ คือ ถ้างานวิจัยเชิงปริมาณเปรียบเป็นรถยนต์
Regression Analysis ก็คือ “เครื่องยนต์หลัก” นั่นเองครับ 🚗

4 บทบาทสำคัญของ Regression Analysis ในงานวิจัย

1. ใช้อธิบายความสัมพันธ์ของตัวแปร

นี่คือบทบาทพื้นฐานที่สำคัญที่สุดครับ

Regression ช่วยให้เราเห็นว่า

• ตัวแปรไหนมีผล
• ส่งผลทางบวกหรือลบ
• ส่งผลแรงแค่ไหน

ตัวอย่างเช่น

งานวิจัยด้านการศึกษาอาจพบว่า

• แรงจูงใจในการเรียน → ส่งผลเชิงบวกต่อผลสัมฤทธิ์
• ความเครียด → ส่งผลเชิงลบต่อคะแนนสอบ

สิ่งเหล่านี้ช่วยให้นักวิจัย “อธิบายปรากฏการณ์” ได้อย่างมีหลักฐานรองรับครับ

2. ใช้ทดสอบสมมติฐานการวิจัย

เวลาเราตั้งสมมติฐานว่า

“ตัวแปร X มีอิทธิพลต่อตัวแปร Y”

Regression จะเข้ามาช่วยพิสูจน์ว่า

• จริงหรือไม่
• มีนัยสำคัญทางสถิติหรือเปล่า
• เชื่อถือได้มากน้อยแค่ไหน

ตรงนี้แหละครับที่อาจารย์ที่ปรึกษาหลายคนให้ความสำคัญมาก เพราะมันเชื่อมระหว่าง “ทฤษฎี” กับ “ข้อมูลจริง”

3. ใช้ทำนายแนวโน้มในอนาคต

นี่คือจุดที่ Regression เท่มากครับ 😎

เพราะมันไม่ได้แค่บอกว่า “อะไรสัมพันธ์กับอะไร”
แต่มันยังช่วย “พยากรณ์” ได้ด้วย

เช่น

• ทำนายพฤติกรรมผู้บริโภค
• คาดการณ์ยอดขาย
• ประเมินผลการดำเนินงานองค์กร
• พยากรณ์ความเสี่ยงทางสุขภาพ

นี่จึงเป็นเหตุผลที่ทั้งนักวิจัย ภาคธุรกิจ และหน่วยงานรัฐนิยมใช้ Regression Analysis กันเยอะมากครับ

4. ใช้ควบคุมตัวแปรแทรกซ้อน

ข้อดีที่หลายคนมองข้ามคือ Regression สามารถ “ควบคุมผลกระทบ” ของตัวแปรอื่นๆ ได้ครับ

ยกตัวอย่าง

ถ้าเราศึกษาว่า “ชั่วโมงอ่านหนังสือ” มีผลต่อคะแนนสอบไหม
แต่จริงๆ อาจมีตัวแปรอื่นแทรก เช่น

• ฐานะครอบครัว
• คุณภาพโรงเรียน
• ความเครียด

Regression จะช่วยแยกผลกระทบของแต่ละตัวแปรออกจากกัน ทำให้ผลวิเคราะห์แม่นยำขึ้นครับ

ประเภทของ Regression Analysis ที่ใช้บ่อย

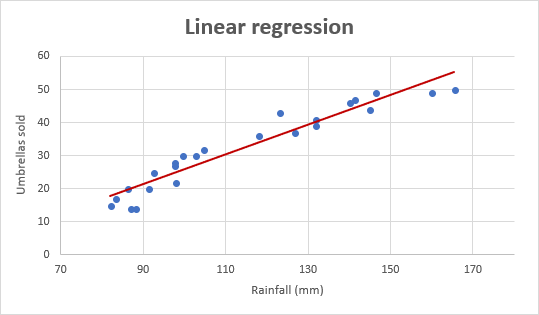
Linear Regression

ใช้เมื่อมีตัวแปรอิสระ 1 ตัว
เหมาะกับงานวิเคราะห์พื้นฐานครับ

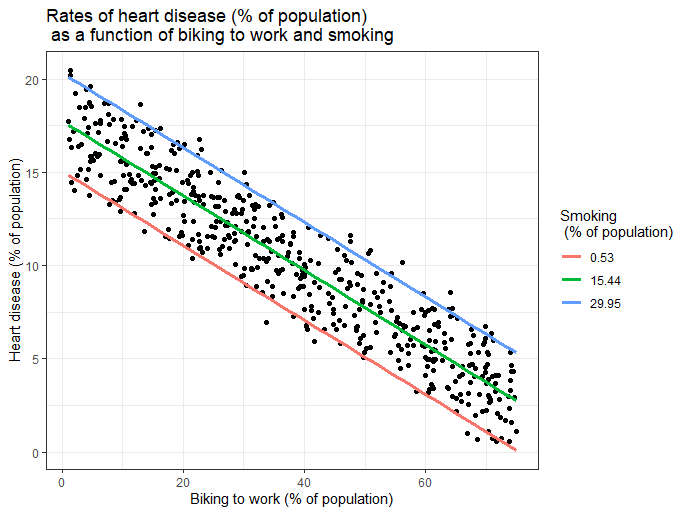
Multiple Regression

ตัวฮิตของงานวิจัยสายสังคมศาสตร์และบริหารครับ
ใช้เมื่อมีหลายปัจจัยร่วมกัน

เช่น

• คุณภาพบริการ
• ราคา
• โปรโมชั่น

ที่ส่งผลต่อความพึงพอใจลูกค้า

Logistic Regression

ใช้เมื่อผลลัพธ์เป็น “กลุ่ม”

เช่น

• ซื้อ / ไม่ซื้อ
• ผ่าน / ไม่ผ่าน
• ป่วย / ไม่ป่วย

Hierarchical Regression

ใช้เมื่อต้องการวิเคราะห์อิทธิพลแบบเป็นขั้นตอน
เหมาะกับงานวิจัยที่มีกรอบแนวคิดซับซ้อนครับ

⚡ ถ้าอ่านมาถึงตรงนี้แล้วยังรู้สึกมึนๆ หรืออยากหาคนช่วย รับทำวิจัย แบบมืออาชีพ ที่การันตีผลงาน ทักหาพี่ได้เลยนะครับ
พี่ช่วยดูตั้งแต่โครงร่าง วิเคราะห์ SPSS ไปจนถึงสรุปผลแบบดูแลจนผ่านครับ

Regression Analysis ใช้ได้กับงานวิจัยด้านไหนบ้าง

ด้านการศึกษา

• วิเคราะห์ปัจจัยที่มีผลต่อผลการเรียน
• ศึกษาประสิทธิภาพการสอน
• วิเคราะห์พฤติกรรมผู้เรียน

ด้านบริหารธุรกิจ

• วิเคราะห์ความพึงพอใจลูกค้า
• ศึกษาปัจจัยที่มีผลต่อยอดขาย
• วิเคราะห์ความภักดีต่อแบรนด์

ด้านสังคมศาสตร์

• ศึกษาพฤติกรรมมนุษย์
• วิเคราะห์ปัจจัยทางสังคม
• ประเมินทัศนคติและการตัดสินใจ

ด้านสาธารณสุข

• วิเคราะห์ปัจจัยเสี่ยงโรค
• ประเมินมาตรการสุขภาพ
• ทำนายผลลัพธ์ด้านสุขภาพ

ข้อควรระวังในการใช้ Regression Analysis

อันนี้สำคัญมากครับ เพราะหลายคนพังตรงนี้

อย่าคิดว่า Regression พิสูจน์ “เหตุและผล” ได้ 100%

Regression บอกได้ว่า “มีความสัมพันธ์”
แต่ไม่ได้แปลว่า “เป็นสาเหตุโดยตรง” เสมอครับ

ต้องตรวจสอบสมมติฐานก่อนทุกครั้ง

เช่น

• Multicollinearity
• Normality
• Linearity
• Homoscedasticity

ถ้าไม่ตรวจ งานวิจัยอาจโดนอาจารย์ถามจนเหงื่อตกครับ 😅

อย่าแปลผลเกินจริง

หลายคนเห็น Sig. < .05 แล้วดีใจสุดชีวิต
แต่ลืมดูว่า Effect Size เล็กมาก

สรุปสุดท้าย “มีนัยสำคัญ แต่ใช้งานจริงแทบไม่มีผล”

อันนี้เจอบ่อยมากครับ

มุมมองจากพี่ (ประสบการณ์ 15 ปี)

พี่เคยเจอนักศึกษาปริญญาโทคนหนึ่งครับ
ทำ Regression ออกมาสวยมาก ค่า Sig. ผ่านทุกตัว แต่พอโดนอาจารย์ถามว่า

“แล้วตัวแปรนี้มีผลเชิงทฤษฎียังไง”

น้องเงียบทั้งห้องเลยครับ 😂

สุดท้ายต้องกลับไปแก้ Framework ใหม่ทั้งหมด

สิ่งที่พี่อยากฝากคือ

“Regression ที่ดี ไม่ใช่แค่ตัวเลขสวย แต่ต้องอธิบายเชิงทฤษฎีได้ด้วยครับ”

เพราะงานวิจัยที่ดี ต้องมีทั้ง

• หลักสถิติ
• หลักวิชาการ
• และเหตุผลเชิงตรรกะ

ครบทั้ง 3 อย่างครับ

ตารางสรุปบทบาทของ Regression Analysis

บทบาท	ความสำคัญ
อธิบายความสัมพันธ์	เข้าใจปัจจัยที่มีผล
ทดสอบสมมติฐาน	ยืนยันทฤษฎี
ทำนายแนวโน้ม	สนับสนุนการตัดสินใจ
ควบคุมตัวแปร	เพิ่มความแม่นยำ
สนับสนุนเชิงนโยบาย	นำผลวิจัยไปใช้ได้จริง

แนวทางใช้ Regression Analysis ให้มีคุณภาพ

พี่แนะนำว่าให้น้องๆ ทำตามนี้ครับ

1. ตั้งคำถามวิจัยให้ชัด
2. เลือก Regression ให้เหมาะ
3. ตรวจสอบสมมติฐานทุกครั้ง
4. ใช้ทฤษฎีรองรับผลวิเคราะห์
5. แปลผลอย่างตรงไปตรงมา

แค่นี้งานวิจัยก็ดูน่าเชื่อถือขึ้นเยอะแล้วครับ

สรุป

Regression Analysis ไม่ใช่แค่เครื่องมือคำนวณทางสถิติ แต่เป็น “หัวใจสำคัญ” ของงานวิจัยเชิงปริมาณครับ

มันช่วยให้นักวิจัยสามารถอธิบาย ทดสอบ และทำนายปรากฏการณ์ต่างๆ ได้อย่างเป็นระบบ และมีหลักฐานรองรับ

แต่สิ่งสำคัญที่สุด คือการใช้ Regression อย่างถูกต้อง มีกรอบแนวคิดรองรับ และแปลผลอย่างมีความรับผิดชอบครับ

จำไว้นะครับ
“ตัวเลขที่สวย ไม่สำคัญเท่าความจริงที่อธิบายได้” 👍

“วิเคราะห์ Regression แล้วงง? ให้พี่ช่วยดู SPSS และงานวิจัยแบบมืออาชีพ ดูแลจนผ่านครับ”

FAQ: คำถามที่พบบ่อยเกี่ยวกับ Regression Analysis